命題
18
5
つの図形の辺を定めて,それらを互いに比較すること。
AB
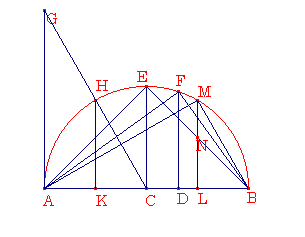
を与えられた球の直径とし、ACとCBが等しくなるようにCで切り,ADがDBの2倍となるようにDで切る。AB上に半円AEBを描き,CとDからABに垂直にCEとDFを描き、AF,FB,EBを結ぶ。AD
はDBの2倍であるので、ABはBDの3倍である。反対に(反転比より)、BAはADの1.5倍である。 ところが,BAはADに対するのと同様に、BA上の正方形はAF上の正方形に対する。なぜなら、△AFBは△AFDと等角だからである。従って、BA上の正方形はAF上の正方形の1.5倍である。 ところが,球の直径上の正方形もまた、角錐の辺上の正方形の1.5倍である。また、ABは球の直径である。よって、AFは角錐の辺と等しい。また、
ADはDBの2倍であるので、ABはBDの3倍である。ところが,ABがBDに対するのと同様に、AB上の正方形正方形はBF上の正方形に対する。従って、AB上の正方形はBF上の正方形の3倍である。ところが、球の直径上の正方形もまた、立方体の
1辺上の正方形の3倍である。そして、ABは球上の直径である。従って、BFは立方体の辺である。また、
ACはCBに等しいので、ABはBCの2倍である。ところが、ABがBCに対するのと同様に、AB上の正方形はBE上の正方形に対する。従って、AB上の正方形はBE上の正方形の2倍である。 ところが、球の直径上の正方形もまた、正8面体の1辺上の正方形の2倍である。そして、ABは与えられた球の直径である。従って,BEは正8面体上の辺である。次に、点
Aから線分ABに垂直にAGを描き、AGとABを等しくし,GCを結び、HからABに垂直にHKを描く。 そのとき、GAはABに等しく、GAがACに対するのと同様に、HKはKCに対するので、GAはACの2倍である。従って、HKもまたKCの2倍である。 よって、HK上の正方形はKC上の正方形の4倍である。従って、HKとKC上の正方形の和,つまり、HC上の正方形はKC上の正方形の5倍である。ところが
,HCはCBに等しい。よって、BC上の正方形はCK上の正方形の5倍である。また、ABはCBの2倍であり、ADはDBの2倍である。従って、残りのDBは残りのDCの2倍である。 よって、BCはCDの3倍である。従って、BC上の正方形はCD上の正方形の9倍である。ところが、BC上の正方形はCK上の正方形の5倍である。よって、CK上の正方形はCD上の正方形より大きい。従って、CKはCDより大きい。 CLをCKに等しくし,LからABに垂直にLMを描き,MBを結ぶ。今
,BC上の正方形はCK上の正方形の5倍であり,ABはBCの2倍であり、KLはCKの2倍である。従って、AB上の正方形はKL上の正方形の5倍である。ところが、球の直径上の正方形もまた、正20面体が描かれている円の半径上の正方形の5倍である。また、ABは球の直径である。従って、KLは正20面体が描かれている円の半径である。従って、KLは言った円に内接する6角形の1辺である。 また、球の直径は6角形の1辺と同じ円に内接する10角形の2辺の和であり、ABは球の直径であり,KLは6角形の1辺であり、AKはLBに等しい。従って、線分AKとLBは互いに、その上に正20面体が描かれている円に内接する10角形の1辺である。また、LBは10角形に属するのと同様にMLは6角形に属する。なぜなら、MLはKLに等しいからである。それはまた、中心から同じ距離のHKに等しく,線分HKとKLの両方はKCの2倍である。従って,MBは5角形に属する。ところが、5角形の1辺は20面体の1辺である。従って、
MBは20面体に属する。今
,FBは立方体の1辺であり,それがNで外中比に切られ,NBは大きい部分とするので、NBは12面体の1辺である。 また、球の直径上の正方形は角錐のAF上の正方形の1.5倍であり、8面体のBE上の正方形の2倍であり,立方体の辺FB上の正方形の3倍であることは証明されているので、従って、球の直径上の正方形を6つに分けた部分と,角錐の1辺上の正方形を4つと、8面体の1辺上の正方形を3つと、立方体の1辺上の正方形を2つもつ。 従って、角錐の1辺上の正方形は8面体の1辺上の正方形の3分の4倍であり、立方体の1辺上の正方形の2倍であり,8面体の1辺上の正方形は立方体の1辺上の正方形の1.5倍である。 3つの図形、角錐、8面体、立方体の辺は互いに、有理数の比をなす。ところが、残りの
2つ、20面体の辺と12面体の辺は互いにもまたは前述の辺にも有理数の比をなさない。なぜなら、それらは無理線分であり,1つは劣線分、もう1つは余線分だからである。20面体の辺MBは12面体の辺NBより大きいこと、このことは証明できる。FDBは△FABと等角であるので比例し,DBがBFに対するのと同様にBFはBAに対する。また、3線分は比例する。1つ目は3つ目に対するのと同様に1つ目上の正方形は2つ目上の正方形に対するので、DBはBAに対するのと同様に、DB上の正方形はBF上の正方形に対する。従って、逆に、ABがBDに対するのと同様にFB上の正方形はBD上の正方形に対する。 ところが,ABはBDの3倍である。よって、FB上の正方形はBD上の正方形の3倍である。 ところが、AD上の正方形もまた,DB上の正方形の4倍である。なぜならば、ADはDBの2倍だからである。よって、AD上の正方形はFB上の正方形より大きい。よって、ADはFBより大きい。従って、ALはFBよりはるかに大きい。また、
ALが外中比で切られたとき、KLは大きい部分である。なぜなら、LKは6角形に属しており、KAは10面体に属していて、また、FBが外中比で切られたとき、NBは大きい部分である。従って、KLはNBより大きい。 ところが、KLはLMと等しい。従って、LMはNBより大きい。 従って、20面体の辺MBは12面体の辺NBよりはるかに大きい。
補助定理
次に、今言った5つの図形のほかに等辺で等角な互いに等しい図形によって囲まれる図形はないことをいう。 なぜなら、立体角は2つの三角形または平面では作ることができないからだ。 3つの三角形で角錐の角、
4つの三角形で8面体の角、5つの三角形で20面体の角がつくられる。ところが、1つの立体角は1点で一緒になる6つの等辺で等角の三角形では作ることができない。なぜなら、等辺の三角形の角は直角の3分の2倍だからであり、6つは4直角に等しいだろう。このことは、不可能である。なぜなら、どの立体角も4直角より小さい角によって構成されるからである。 同じ理由から、立体角は6つより多くの平面角によって作ることはできない。 立方体の角は3つの正方形によって構成される。ところが、立体角が4つによって構成されることは不可能である。なぜなら、それらもまた、4直角になるからである。 正12面体の角は3つの等辺で等角の5角形によって構成される。ところが、どの立体角も4つで構成することは不可能である。なぜなら、等辺の5角形の角は直角と5分の1だからであり、4つの角は4直角よりも大きいだろう。このことは不可能である。 同じ理由より、立体角は他の多角形によって構成されることはない。 ところが、その等辺で等角の5角形の角は、直角と5分の1であるということはこのように証明しなければならない。 ABCDEを等辺で等角の5角形とし、それを円ABCDEが外接し,Fを中心とし,FA,FB,FC,FD,FEを結ぶ。 従って、それらは、5角形の角A,B,C,D,Eを2等分する。そして、Fの角は4直角に等しく、互いに等しいので、それらの1つ、∠AFBは直角より5分の1小さい。従って、残りの角∠FABと∠ABF直角と5分の1になる。ところが、∠FABは∠FBCに等しい。従って、5角形の角の∠ABC全体は直角と5分の1である。証明終了