命題11
もし等辺の五角形がその直径を有理線分とする円に内接するなら、五角形の辺は劣線分という
,無理線分となる.
有理線分を直径とする円
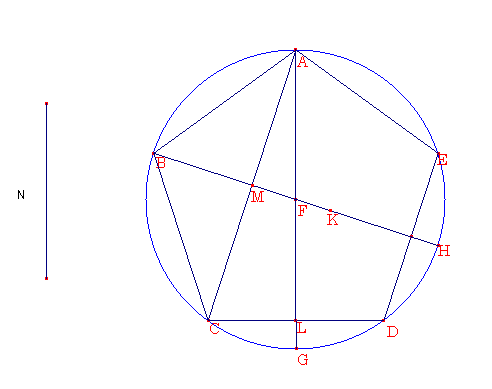
ABCDE に等辺の五角形ABCDE が内接しているとする.五角形の辺は,劣線分という,無理線分であるとする.円の中心Fをとって、 AF と FB を結ぶ.そしてFを点GとHまで延長して,ACが結ばれ,、そして FK を AF の4分の1とする.今, AF は有理線分である.そのために FK は同じく有理線分である.けれども BF は同じく有理線分である.そのために BK 全体は有理線分である.そして、弧ACG は弧ADG と等しい.そして,ABCはAEDと等しいから,残りの CG は残りの GDと等しい.そして、AD を結ぶと,Lにおける角が直角であり,CDはCLの2倍であるといえる.同じ理由のためにMにける角が直角であり,ACはCMの2倍となる.そのために,角 ALC は角 AMF と等しく,そして角 LAC は2つの三角形ACL, AMF と共通なので,残っている角 ACL は残っている角MFAと等しい.そのために,三角形ACL は,三角形AMF と等角である.そのために、相似であるから,LCがCAに対するように,MF が FAに対する.そして,もし前項の2倍をとったとしたら,LC の2倍が CA にに対するように, MF の2倍が FA に対する.けれども、 MF の2倍が FA 似たいするように,MFがFAの2分の1に対する.そのために同じく,LCの2倍がCAに対するように, MF が FA の半分に対する.そして,もし後項の半分をとったとしたら,LCの2倍がCAの半分に対するように,MFがFAの4分の1に対する.そしてDCはLCの2倍である.CMは CA の2分の1である.そして FK は FA の4分の1である.そのためにDCがCMに対するように,MFがFKに対する.よって,DC,CMの和がCMに対するように,MKがKFに対する.そのために,DC,CM上の正方形の和がCM上の正方形に対するように, MK の上の正方形が KF上の正方形に対する.そして、五角形の2辺に対する線分,例えばACが外中比に分けられるならば,より大きい部分が五角形の辺と等しい、すなわちDCと等しいので,大きい部分を全体の半分に追加したものの上の正方形は全体の半分の上の正方形の5倍であり,CMはAC全体の半分であるから,1つの直線としたとき,DCM上の正方形は,CM上の正方形の五倍である.けれども1つの直線としたときに,DCM上の正方形がCM上の正方形に対するように,MK上の正方形がKF上の正方形に対することが,証明されている.そのために MK の上の正方形は KF の上の正方形の五倍となる.けれども,直径が有理線分であるから, KF上の正方形は有理面積である.そのために MK上の正方形は同じく有理面積である.そのために MK上の正方形も有理面積である.そして,BF が4倍の FK であるので,そのために BK が KF の五倍である.そのために BK上の正方形は KF上の正方形の25倍である.けれども MK上の正方形は KF上の正方形の五倍である.そのために BK上の正方形はKM上の正方形の五倍である.そのために BK上の正方形はKM上の正方形に対して,平方数が平方数に対する比率を持っていない.そのために BK は KMと長さにおいて通約できない.そして,それらのそれぞれが有理線分である.そのために BK とKMは平方のみで通約できる有理線分である.けれども、もし有理線分から全体と平方だけで通約できる有理線分がとられるならば,残りは無理線分である.すなわち余線分である.そのために,MBは余線分である.そして,MKがMBに対する付加である.次に,MBが同じく4番目の余線分であるとする.N上の正方形をBK上の正方形からKM上の正方形を引いたときの差と等しくさせる.そのためにBK上の正方形は,KM上の正方形よりN上の正方形だけ大きい.そして,KFはFBと通訳でき,KBはFBと通約できる.けれども BF は BH と通約できる.そのために BK は BH で同じく通約できる.そして、 BK上の正方形がKM上の正方形の五倍であるから,そのために BK上の正方形はKM上の正方形の五分の1となる.そのために,言いかえると,BK上の正方形はN上の正方形の五分の4となる.そしてこれは平方数が平方数に対する比率とは言えない.そのために BK はNと通約できない.そのために BK上の正方形は BKと通約できない線分上の正方形の分だけ,KM上の正方形が大きい.そのために,BK 全体の上の正方形は付加されたKM上の正方形より,BKと通約できない線分上の正方形だけ大きく,MBは4番目の余線分である.なぜならば,BK全体は,定められた有理線分BHと通約できるからである.けれども有理線分と4番目の余線分によって囲まれる矩形は,無理面積であり,それと等しい正方形の辺は劣線分と呼ばれる無理線分である.けれども,HBがBAに対するから,AB上の正方形は矩形HBMと等しい.なぜなら,AH が結ばれると,三角形ABH は三角形ABMと等角だからである.そのために五角形の辺ABは劣線分と呼ばれる無理線分となる.もし等辺の五角形がその直径を有理線分とする円に内接するなら、五角形の辺は劣線分という,無理線分となる.証明終了