前で述べたように、球の中に正8面体をつくり、球の直径上の正方形が8面体の1辺上の正方形の2倍であることを証明する。

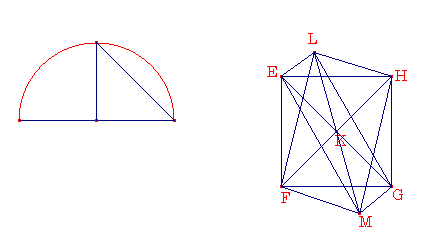
　与えられた球の直径ABをおき、Cで2等分する。AB上に半円ADBを描き、ABに垂直にCからCDを描き、DBを結ぶ。　DBに辺がそれぞれ等しい正方形EFGHをおき、HFとEGを結び,正方形EFGHの平面に垂直にKから線分KLをひく。そして、平面の反対側を通るようにKMを延長させる。　線分KLとKMがそれぞれ、EK,FK,GK,HKの1つに等しいようにKLとKMが切られ,LE、LF、LG、LH、ME、MF、MG、MHを結ぶ。

　そのとき、KEはKHと等しく、∠EKHは直角であるので、HE上の正方形はEK上の正方形の2倍である。同様に、LKはKEと等しく、∠LKEは直角であるので、EL上の正方形はEK上の正方形の2倍である。

　ところが、HE上の正方形もまた、EK上の正方形の2倍であることが証明されている。従って、LE上の正方形はEH上の正方形と等しい。よって、LEはEHと等しい。同じ理由から,LHもまたHEと等しい。　従って、三角形LEHは等辺である。　同様に、正方形EFGHの辺が底辺であり、点L,Kが頂点である残りの三角形もまたそれぞれ等辺であることが証明できる。従って、８つの等辺三角形よってつくられた正8面体が構成される。

　次に、与えられた球に囲まれ,球の直径上の正方形が正8面体の1辺上の正方形の2倍であることを証明する必要がある。

　3つの線分LK,KM,KEは互いに等しいので、LM上に描く半円はEを通る。また、同じ理由から,もし、LMが固定されたままで、半円が回転され、動き始めたところから,同じ点に戻るなら,そのとき、それもまた点F,G,Hとを通り、正8面体は球に囲まれるであろう。

　LKはKMに等しく、KEは共通であり、それらは直角を持つので、底辺LEは底辺EMに等しい。

　また、半円の中にあるので∠LEMは直角であるので,LM上の正方形はLE上の正方形の2倍である。

　また、ACはCBに等しいので、ABはBCの2倍である。ところが、ABはBCに対するのと同様に、AB上の正方形はBD上の正方形に対する。従ってAB上の正方形はBD上の正方形の2倍である。　ところが、LM上の正方形もまた、LE上の正方形の2倍であることが証明されている。そして、DB上の正方形はLE上の正方形に等しい。なぜなら、EHはDBに等しいからである。従って、AB上の正方形はLM上の正方形に等しい。よってABはLMに等しい。　また、ABは与えられた球の直径である。従って、LMは与えられた球の直径に等しい。　従って、正8面体は球に囲まれ,球の直径上の正方形が正8面体の1辺上の正方形の2倍であることが同時に証明された。

　証明終了

第13巻命題13へ　第13巻命題15へ　第13巻目次へ