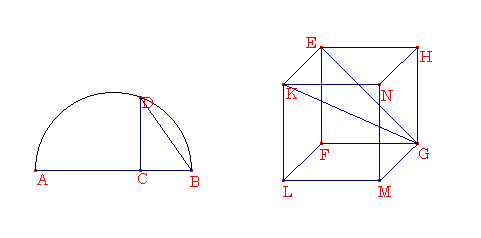
命題15
立方体を作り
,角錐のように球によって囲み,そして球の直径の上の正方形が立方体の辺の正方形の3倍であることを証明する.
所定の球の直径
ABを書いて,そしてACがCBの2倍であるように,点Cを置く.AB の上に半円形ADBを書き,CからABに対して直角をなすようにCDを引いて,そしてDBと結ぶ.そして,DBに等しい辺を持つ正方形EFGHを作り,E,F,G,Hから正方形EFGHの面に垂線EK,FO,GM,HNが引かれ,そのそれぞれから,EF,FG,GH,GEに1だけ等しく,EK,FO,GM,HNが切り取られて,KO,EK,FL,GMが結ばれたとする.そのために6つの等しい正方形によって囲まれる立方体FNが組み立てられた.それを所定の球でで囲み,そして球の直径の上の正方形が立方体の辺の上の正方形の3倍であることを証明する.KGとEGを結ぶ.それなら,面EGに対してKEが垂直であり,線分EGに対して垂直であり,角KEGは垂直であるから,KG上に書かれる半円は,点Eをとおる。そして,FO,FEのそれぞれは,GFと垂直であるから,GFは面FKに対しても垂直である.この理由のために同じく,GKの上に書かれた半円形はFを通るであろう.同様にそれは同じく立方体の残っている点も通るであろう.よってもし,KGを固定されている状態で半円が回転され,そしてそれが回転し始めた同じ場所に戻ってくるならば,立方体は球によって囲まれるであろう.次にそれが所定の球に囲まれることを証明して行く.GFがFEと等しく,そしてFにおいての角が直角なので,そのためにEGの上の正方形はEFの上に正方形の2倍である.けれども,EFはEKと等しい.そのために,EGの上の正方形はEKの上の正方形の2倍である.そのために,GEとEKの上の正方形の和,すなわちGKの上の正方形のは,EKの上の正方形の3倍である.そして,AB がBCの3倍であり,ABがBCに対するように,AB の上の正方形が BD の上の正方形に対するから,そのために,ABの上の正方形はBDの上の正方形の3倍である.けれどもGKの上の正方形が同じく,KEの上の正方形の3倍であることは証明した.そして,KEはDBと等しいされた.そのためにKGが同じくABと等しい.そして,ABは所定の球の直径である.従ってKGが同じく所定の球の直径と等しい.そのために立方体は所定の球によって囲まれた.そして,球の直径の上の正方形が立方体の辺の上の正方形の3倍であることが合わせて証明された.証明終了