命題8
もし辺が等しく,角も等しい五角形があったとき
,2つの線分が隣り合う2つの角を分けるならば,それらはお互いに外中比で分けられ,それらの大きい部分は五角形の辺と等しい.

辺が等しく
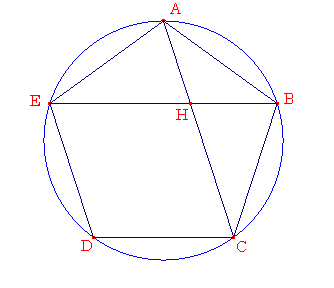
,角も等しい五角形ABCDEにおいて,点Hで互いに交わる線分AC,BEが隣り合う2つの角A,Bを分けるとする.それらは点Hにおいて外中比にわけられ,それらのより大きい部分は五角形の辺と等しくなる。五角形 ABCDE に円 ABCDE が外接するとする。すると、2つの直線 EA と AB が2つの直線 AB と BC と等しくなり,そして,それらが等しい角を含んでいるので、そのために底辺 BE は底辺ACと等しくなり,三角形 ABE は三角形ABCと等しくなり,残りの角は残りの角と等しくなり,すなわち等しい辺が対する角はそれぞれ等しくなる。そのために角 BAC は角 ABE と等しい.そのために角 AHE は角 BAH の2倍となる.けれども角 EAC は同じく角 BAC の2倍である.なぜならば,弧EDC は同じく弧CB の2倍であるからである。そのために角 HAE は角 AHE と等しい。それために直線 HE は同じく EA,すなわちAB と等しい。そして、直線BAが AE と等しいことから,角 ABE は同じく角 AEB と等しい。けれども角 ABE は角 BAH と等しいと証明された、そのために角 BEA は同じく角 BAH と等しい。そして角 ABE は2つの三角形ABE,ABH と共通である.そのために残っている角 BAE は残っている角 AHB と等しい。そのために三角形ABE は三角形ABH に対して,角が等しい。そのために、相対的に,EB が BA に対するように,AB が BHに対する。けれども BA は EH と等しい.そのために,BEがEHに対するように,BE は EH に対する.そして BE は EHよりおおきい.そのために EH は HB より大きい.そのために BE はHにおいて外中比に分けられ,大きい辺であるHEは五角形の辺と等しい.同様にACが同じくHにおいて外中比に分けられ,大きい辺であるCHは五角形の辺と等しい.もし辺が等しく,角も等しい五角形があったとき,2つの線分が隣り合う2つの角を分けるならば,それらはお互いに外中比で分けられ,それらの大きい部分は五角形の辺と等しい.証明終了