命題20
2つの数の間に1つの比例中項があるならば、その数は相似な平面数である。
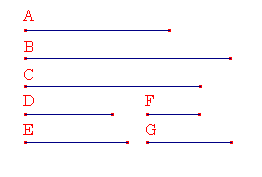
2つの数AとBの間に1つの比例中項Cがあるとする。
AとBが相似な平面数であることをいう。
AとCと同じ比を持つ数の最小数、DとEを取る。EがCを割り切ると同じ回数でDはAを割り切る。propositionⅦ.33、propositionⅦ.20
DがAを割り切るようにFに単位があるとする。FにDを掛けてAを作る。つまりAは平面数であり、DとFはその辺である。
再度、CとBと同じ比を持つ数の最小数、DとEを取るから、それゆえにEはBを割り切ると同じ回数でDはCを割り切る。propositionⅦ.20
EがBを割り切るようにBに単位があるとする。EはBをGの単位により割り切る。それゆえにGにEを掛けてBを作る。
それゆえにBは平面数であり、EとGはその辺である。それゆえにAとBは平面数である。
次にそれらはまた相似であることをいう。
FにDを掛けてAを作り、Eを掛けてCを作るから、それゆえにDはEに対し同じようにAはCに対し、つまりCはBに対する。propositionⅦ.17
再度、EにFとGを掛けてそれぞれCとBを作るから、FはGに対し同じようにCはBに対する。しかしCはBに対し同じようにDはEに対し、それゆえにDはEに対し同じようにFはGに対する。そして入れ替えてDはFに対し同じようにEはGに対する。propositionⅦ.17、propositionⅦ.13
それゆえにAとBは、それらの辺が比例しているために、相似な平面数である。
それゆえに、2つの数の間に1つの比例中項があるならば、その数は相似な平面数である。
証明終了