命題2
もし、線分上の正方形が
,その上の線分上の正方形の5倍であるならば、その線分の2倍が外中比で切られたとき長い線分は最初の線分の残りの一部である。
線分
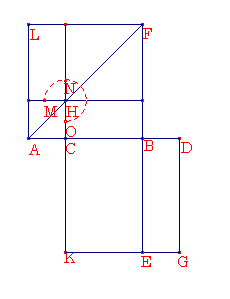
AB上の正方形は線分AC上の正方形の5倍であるとし、CDはACの2倍とする。CDが外中比で切られるとき、長い線分はCBとする。正方形AFとCGをABとCD上にそれぞれかき、AF上に図形を描き、BEをひく。 今BA上の正方形はAC上の正方形の5倍であるのでAFはAHの5倍である。従ってノーモンMNOはAHの4倍である。また、DCはCAの2倍であるのでDC上の正方形はCA上の正方形の4倍である。すなわち、CGはAHの4倍である。ところが、ノーモンMNOもまたAHの4倍であるのでノーモンMNOはCGに等しい。また、DCはCAの2倍であり,DCはCKに等しく、ACはCHに等しいので、KBもまたBHの2倍である。ところが、LHとHBの和もまた、HBの2倍であるのでKBはLHとHBの和に等しい。ところが、ノーモンMNO全体はまた、CG全体に等しいことが証明されているので、残りのHFはBGに等しい。 また、BGはDBからなる短形CDである。なぜなら、CDはDGに等しくHFはCB上の正方形であるからである。従って、DBからなる短形CDはCB上の正方形に等しい。従ってDCはCBに対するのと同様にCBはBDに対する。しかし、DCはCBより大きい。従ってCBもまたBDより大きい。 従って線分CDが外中心で切られたときCBは大きい方の線分になる。
補助定理
ACの2倍がBCより大きいことはこのようにして証明される。 もしそうでないならば、可能であるなら、BCがCAの2倍である。 従ってBC上の正方形はCA上の正方形の4倍である。よってBCとCA上の正方形の和はCA上の正方形の5倍である。ところが、仮定よりBA上の正方形もまたCA上の正方形の5倍である。従って、BA上の正方形はBCとCA上の正方形の和に等しい。これは不可能である。従って、CBはACの2倍ではない。同様にCBより小さい線分もCAの2倍でないことが証明できる。従ってACの2倍はCBより大きい。 従って、もし、線分上の正方形が,その上の線分上の正方形の5倍であるならば、その線分の2倍が外中比で切られたとき長い線分は最初の線分の残りの一部である。
証明終了