もし直線が、外中比で分けられるならば,全体の上の正方形と，そしてより小さい部分の上の正方形との和は，より大きい部分の上の正方形の３倍である。

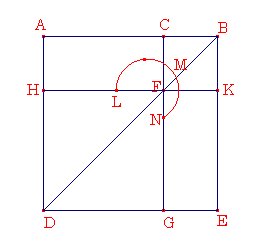
線分AB をＣにおいて外中比に分けられたとし、そしてＡＣをより大きい部分とする。AB と BC の上の正方形の和が CA の上に正方形の３倍であるとする。AB の上に正方形ADEB を作図されたとする。それから、 AB がＣにおいて外中比に分けられたとする。そしてＡＣがより大きい部分であるので、そのために ABC はＡＣの上の正方形と等しい。そして ABC は AKと等しく,ＡＣの上の正方形はHGと等しい.そのために AK は HG と等しい.そして、 AF が FE と等しい。そして，その両方へ CK が足されたとする.すると， AK 全体が CE 全体と等しい。そのために AK と CE の和は AK の２倍となる。けれども AK と CE の和は gnomon LMN と正方形の CK の和である。そのために gnomon LMN と正方形 CKの和は AK の２倍となる。けれども、さらに、 AK は同じく HG と等しいと証明た。そのために gnomon LMN と正方形 CK ，HG の和は正方形HG の３倍である。そして gnomon LMN と正方形 CK ，HG の和は正方形AE 全体と CK の和であり，それはAB,BCの上の正方形の和であり, HG はＡＣの上の正方形である。そのために AB と BC の上の正方形の和はＡＣの上の正方形の３倍である。もし直線が、外中比で分けられるならば,全体の上の正方形と，そしてより小さい部分の上の正方形との和は，より大きい部分の上の正方形の３倍である。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　証明終了

第13巻命題3へ　第13巻命題5へ　第13巻目次へ