命題16
「与えられた円に等辺等角な十五角形を内接させること」

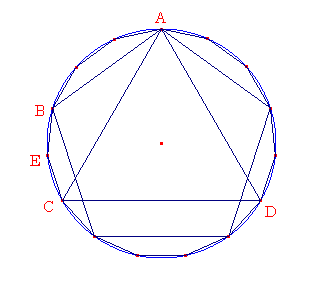
与えられた円をABCDとせよ。
円ABCDに等辺等角な十五角形を内接させることが要求されている。
円ABCDに辺ACをもつ等辺三角形と辺ABをもつ等辺五角形のを内接しなさい。
それゆえ、円ABCDに15の等しい部分があり、円の1/3である弧ABCにそのうちの5つがあり、円の1/5である弧ABにそのうちの3つがあるであろう。それゆえ、残りのBCに等しい部分のうちの2つがあるであろう。EでBCを2等分しなさい。命題Ⅲ.30
それゆえ、弧BE、ECのおのおのは円ABCDの1/15である。
よって、BE、ECを結び、それらに等しい線分を順番に円ABCDに挿入するならば、等辺等角な十五角形がそれに内接しているであろう。
それゆえ、等辺等角な十五角形が与えられた円に内接している。
作業終了
系
そして、この前の五角形の場合のように、円周上の区分点を通って円の接線をひくならば、等辺等角な五角形が円に外接させるであろう。
そして、さらに、五角形の場合にいわれたように、与えられた十五角形に円を内接したり外接させることができる。