命題３２

 

 

２辺が２辺に比例している２つの三角形が１つの角によって結ばれ、それらの対応する辺もまた平行であるならば、三角形の余りの辺は一直線である。

 

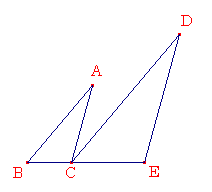
ABCとDCEを２つの辺ABとBCが２つの辺DCとDEに比例している２つの三角形とする。つまりABはACに対し同じようにDCはDEに対し、ABはDCと平行であり、ACはDEと平行である。

 

BCはCEと一直線上にあることをいう。

 

ABはDCと平行であり、直線ACがそれらとあたるから、それゆえに交互の∠BACと∠ACDは互いに等しい。proposition�T．２９

 

同じ理由で∠CDEもまた∠ACDと等しく、だから∠BACは∠CDEと等しい。

 

そして、ABCとDCEは１つの∠Aと等しい１つの∠Dを持ち、等しい角のまわりの辺は比例している、つまりABはACに対し同じようにDCはDEに対する、２つの三角形であるから、それゆえに��ABCは��DCEと対応する角が等しい。それゆえに∠ABCは∠DCEと等しい。proposition�Y．６

 

しかし∠ACDが∠BACと等しいことは証明されていて、それゆえに全体の∠ACEは２つの∠ABCと∠BACの和と等しい。

 

それぞれに∠ACBを加える。それゆえに∠ACEと∠ACBの和と∠BACと∠ACBと∠CBAの和は等しい。

 

しかし∠BACと∠ABCと∠ACBの和は２直角と等しく、それゆえに∠ACEと∠ACBの和もまた２直角と等しい。proposition�T．３２

 

それゆえに直線ACとAC上の点Cにおいて、同じ側にない２つの直線BCとCEは２直角と等しい隣接した∠ACEと∠ACBの和を作る。それゆえにBCはCEと一直線上にある。proposition�T．１４

 

それゆえに、２辺が２辺に比例している２つの三角形が１つの角によって結ばれ、それらの対応する辺もまた平行であるならば、三角形の余りの辺は一直線である。

 

証明終了

 

 

 

第６巻命題３１へ　　第６巻命題３３へ　　第６巻目次へ