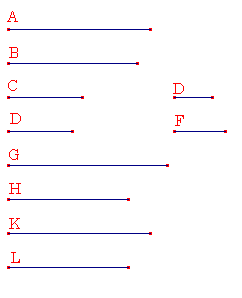
–½‘è‚T
پ@•½–تگ”‚حپAŒف‚¢‚ة‚»‚ê‚ç‚ج•س‚ج”ن‚جگد‚ج”ن‚ً‚à‚آپB

پ@A‚ئB‚ً•½–تگ”‚ئ‚µپAC‚ئD‚ًA‚ج•سپAE‚ئF‚ًB‚ج•س‚ئ‚¹‚وپB
پ@A‚حB‚ة‘خ‚µ‚ؤپA•س‚ج”ن‚جگد‚ج”ن‚ً‚à‚آ‚ئژه’£‚·‚éپB
پ@C‚حE‚ة‘خ‚µ‚ؤپAD‚حF‚ة‘خ‚·‚é”ن‚ھ—^‚¦‚ç‚êپAکA‘±‚µ‚ؤCپAEپADپAF‚ج”ن‚ئ‚ب‚éچإڈ¬‚جگ”GپAHپAK‚ً‚ئ‚èپA‚آ‚ـ‚èپAC‚حE‚ة‘خ‚µ‚ؤپAG‚حH‚ة‘خ‚µپA‚ـ‚½پAD‚حF‚ة‘خ‚µ‚ؤپAH‚حK‚ة‘خ‚·‚éپBproposition‡[پD‚S
پ@D‚ًE‚ة‚©‚¯‚ؤL‚ًچى‚é‚ئ‚¹‚وپB
پ@چ،پAD‚ةC‚ً‚©‚¯‚ؤA‚ًچى‚èپAE‚ً‚©‚¯‚ؤL‚ًچى‚é‚ج‚إپA‚»‚ê‚ن‚¦‚ةپAC‚حE‚ة‘خ‚µ‚ؤپAA‚حL‚ة‘خ‚·‚éپBproposition‡ZپD‚P‚V
پ@‚µ‚©‚µپAC‚حE‚ة‘خ‚µ‚ؤپAG‚حH‚ة‘خ‚µپA‚»‚ê‚ن‚¦‚ةپAG‚حH‚ة‘خ‚µ‚ؤپAA‚حL‚ة‘خ‚·‚éپB
پ@چؤ‚رپAE‚ةD‚ً‚©‚¯‚ؤL‚ًچى‚èپA‚³‚ç‚ةپAF‚ً‚©‚¯‚ؤB‚ًچى‚é‚ج‚إپA‚»‚ê‚ن‚¦‚ةپAD‚حF‚ة‘خ‚µ‚ؤپAL‚حB‚ة‘خ‚·‚éپB
پ@‚µ‚©‚µپAD‚حF‚ة‘خ‚µ‚ؤپAH‚حK‚ة‘خ‚µپA‚»‚ê‚ن‚¦‚ةپAH‚حK‚ة‘خ‚µ‚ؤپAL‚حB‚ة‘خ‚·‚éپBproposition‡ZپD‚P‚V
پ@‚µ‚©‚µپAG‚حH‚ة‘خ‚µ‚ؤپAA‚حL‚ة‘خ‚·‚邱‚ئ‚حڈط–¾‚³‚ê‚ؤ‚¢‚éپB
پ@‚»‚ê‚ن‚¦‚ةپA“™ٹشٹu”ن‚ة‚و‚èپAG‚حK‚ة‘خ‚µ‚ؤپAA‚حB‚ة‘خ‚·‚éپBproposition‡ZپD‚P‚S
پ@‚µ‚©‚µپAG‚حK‚ة‘خ‚µ‚ؤپA•س‚ج”ن‚جگد‚ج”ن‚ً‚à‚آپB
پ@‚»‚ê‚ن‚¦‚ةپAA‚à‚ـ‚½B‚ة‘خ‚µ‚ؤپA•س‚ج”ن‚جگد‚ج”ن‚ً‚à‚آپB
پ@‚»‚ê‚ن‚¦‚ةپA•½–تگ”‚حپAŒف‚¢‚ة‚»‚ê‚ç‚ج•س‚ج”ن‚جگد‚ج”ن‚ً‚à‚آپB
ڈط–¾ڈI—¹