 丂
丂柦戣俆
乽梌偊傜傟偨嶰妏宍偵墌傪奜愙偡傞偙偲乿
 丂
丂
梌偊傜傟偨嶰妏宍傪俙俛俠偲偣傛丅
梌偊傜傟偨嶰妏宍俙俛俠偵墌傪撪愙偡傞偙偲偑梫媮偝傟偰偄傞丅
揰俢丄俤偱慄暘俙俛丄俙俠傪俀摍暘偟側偝偄丅揰俢丄俤偐傜俙俛丄俙俠偵捈妏側俢俥丄俤俥傪傂偒側偝偄丅偦偺偲偒丄偦傟傜偼嶰妏宍俙俛俠偺撪晹偱岎傢傞偐丄慄暘俛俠忋偱岎傢傞偐丄俛俠偺奜晹偱岎傢傞丅柦戣嘥丏10
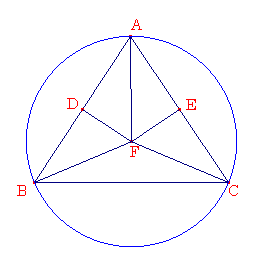
傑偢丄偦傟傜傪俥偱撪晹偱岎傢傞偲偣傛丅俥俛丄俥俠丄俥俙傪寢傃側偝偄丅
偦偺偲偒丄俙俢偼俢俛偲摍偟偔丄俢俥偼嫟捠偱丄捈妏側偺偱丄掙曈俙俥偼掙曈俥俛偲摍偟偄丅柦戣嘥丏係
摨條偵偟偰丄俠俥傕俙俥偲摍偟偄偙偲偑徹柧偱偒傞偺偱丄俥俛傕俥俠偲摍偟偄丅偦傟備偊丄俁慄暘俥俙丄俥俛丄俥俠偼屳偄偵摍偟偄丅
偦傟備偊丄拞怱傪俥丄敿宎傪慄暘俥俙丄俥俛丄俥俠偺偆偪偺侾偮傪傕偭偰偐偐傟傞墌偼巆傝偺揰傕捠傝丄墌偼嶰妏宍俙俛俠偵奜愙偟偰偄傞丅
俙俛俠偺傛偆偵奜愙偡傞偲偣傛丅
 丂
丂
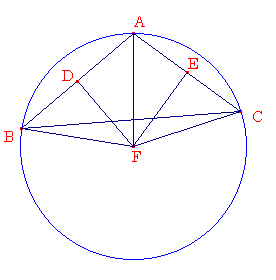
偮偓偵丄俀斣栚偺恾偺傛偆偵俢俥丄俤俥傪慄暘俛俠忋偺俥偱岎傢傞偲偣傛丅俙俥傪寢傃側偝偄丅
偦偺偲偒丄摨條偵偟偰丄揰俥偼嶰妏宍俙俛俠偵奜愙偡傞墌偺拞怱偱偁傞偙偲偑徹柧偱偒傞丅
 丂
丂
偮偓偵丄俁斣栚偺恾偺傛偆偵俢俥丄俤俥傪嶰妏宍俙俛俠偺奜晹偱俥偱岎傢傞偲偣傛丅俙俥丄俛俥丄俠俥傪寢傃側偝偄丅
偦偺偲偒丄傑偨丄俙俢偼俢俛偲摍偟偔丄俢俥偼嫟捠偱丄捈妏側偺偱丄掙曈俙俥偼掙曈俥俛偲摍偟偄丅柦戣嘥丏係
摨條偵偟偰丄俠俥傕俙俥偲摍偟偄偙偲偑徹柧偱偒傞偺偱丄俥俛傕俥俠偲摍偟偄丅偦傟備偊丄拞怱傪俥丄敿宎傪慄暘俥俙丄俥俛丄俥俠偺偆偪偺侾偮傪傕偭偰偐偐傟傞墌偼巆傝偺揰傕捠傝丄墌偼嶰妏宍俙俛俠偵奜愙偟偰偄傞丅
偦傟備偊丄墌偼梌偊傜傟偨嶰妏宍偵奜愙偟偰偄傞丅
嶌嬈廔椆
宯
丂偦偟偰丄墌偺拞怱偑嶰妏宍偺撪晹偵偍偪傞偲偒丄敿墌傛傝戝偒偄愗曅撪偵偁傞偺偱丄妏俛俙俠偼捈妏傛傝彫偝偔丄拞怱偑慄暘俛俠忋偵偍偪傞偲偒丄敿墌偵偁傞偺偱丄妏俛俙俠偼捈妏偱丄墌偺拞怱偑嶰妏宍偺奜晹偵偍偪傞偲偒丄敿墌傛傝彫偝偄愗曅撪偵偁傞偺偱丄妏俛俙俠偼捈妏傛傝戝偒偄偙偲偑柧傜偐偱偁傞丅