 丂
丂柦戣係
乽梌偊傜傟偨嶰妏宍偵墌傪撪愙偡傞偙偲乿
 丂
丂
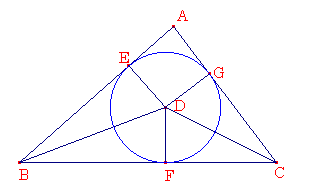
梌偊傜傟偨嶰妏宍傪俙俛俠偲偣傛丅
嶰妏宍俙俛俠偵墌傪撪愙偡傞偙偲偑梫媮偝傟偰偄傞丅
慄暘俛俢丄俠俢偱妏俙俛俠丄俙俠俛傪俀摍暘偟丄偙傟傜傪揰俢偱屳偄偵岎傢傞偲偣傛丅俢偐傜慄暘俙俛丄俛俠丄俠俙偵悅捈側俢俤丄俢俥丄俢俧傪傂偒側偝偄丅柦戣嘥丏俋
偄傑丄妏俙俛俢偼妏俠俛俢偲摍偟偔丄捈妏俛俤俢傕捈妏俛俥俢偲摍偟偄偺偱丄俤俛俢丄俥俛俢偼俀妏偑俀妏偲摍偟偔丄侾曈偑侾曈偲摍偟偄丄偮傑傝摍偟偄妏偺侾偮偵懳偡傞嫟捠偺曈俛俢傪傕偮俀偮偺嶰妏宍偱偁傞丅偦傟備偊丄偦傟傜偼傑偨巆傝偺曈傪巆傝偺曈偲摍偟偔偡傞偱偁傠偆丅偦傟備偊丄俢俤偼俢俥偲摍偟偄丅柦戣嘥丏26
摨條側棟桼偱丄俢俧傕俢俥偲摍偟偄丅
偦傟備偊丄俁慄暘俢俤丄俢俥丄俢俧偼屳偄偵摍偟偄丅偦傟備偊丄拞怱傪俢丄敿宎傪俢俤丄俢俥丄俢俧偺偆偪偺侾偮傪傕偭偰偐偐傟傞墌傕巆傝偺揰傪捠傝丄揰俤丄俥丄俧偵偍偗傞妏偼捈妏偱偁傞偨傔丄慄暘俙俛丄俛俠丄俠俙偲愙偡傞丅
側偤側傜丄墌偑偦傟傜偲岎傢傞側傜偽丄墌偺捈宎偵偦偺椉抂偐傜捈妏偵傂偐傟偨慄暘偼墌偺撪晹偵偍偪傞偙偲偵側傞偱偁傠偆丅偙傟偼晄崌棟偱偁傞偙偲偑徹柧偝傟偨丅偦傟備偊丄拞怱傪俢丄敿宎傪俢俤丄俢俥丄俢俧偺偆偪偺侾偮傪傕偭偰偐偐傟傞墌偼慄暘俙俛丄俛俠丄俠俙偲岎傢傜側偄丅偦傟備偊丄偦傟傜偲愙偟丄墌偼嶰妏宍俙俛俠偵撪愙偡傞丅柦戣嘨丏16丆掕媊嘩丏俆
俥俧俤偺傛偆偵撪愙偡傞偲偣傛丅
偦傟備偊丄墌俤俥俧偼梌偊傜傟偨嶰妏宍俙俛俠偵撪愙偟偰偄傞丅
嶌嬈廔椆