命題6
「与えられた円に正方形を内接させること」

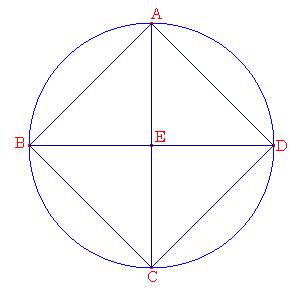
与えられた円をABCDとせよ。
円ABCDに正方形を内接させることが要求されている。
互いに直角な円ABCDの2つの直径AC、BDをひき、AB、BC、CD、DAを結びなさい。
そのとき、Eは中心なので、BEはEDと等しく、EAは共通で、直角なので、底辺ABは底辺ADと等しい。命題Ⅰ.4
同様な理由で、線分BC、CDのそれぞれも線分AB、ADのそれぞれと等しい。それゆえ、四辺形ABCDは等辺形である。
つぎに、それはまた直角であることをいう。
線分BDは円ABCDの直径なので、BADは半円である。それゆえ、角BADは直角である。命題Ⅲ.31
同様な理由で、角ABC、BCD、CDAのそれぞれも直角である。それゆえ、四辺形ABCDは直角である。
しかし、等辺であることも証明されていた。それゆえ、それは正方形である。それゆえ、それは円ABCDに内接している。定義Ⅰ.23
それゆえ、正方形ABCDは与えられた円に内接している。
作業終了