命題2
連続した比例に指示されたと同じ個数で、与えられた比である最小の数を見つけること。
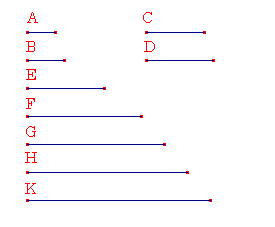
AがBに対する比を与えられた最小の数である比とする。
指示されたと同じ数でAがBに対する比である最小の数である比例する数を見つけることを必要とする。
4つの数を指示されるとする。Cを作るためにAにAを掛け、Dを作るためにBを掛ける。Eを作るためにBにBを掛ける。また、F、G、Hを作るためにAにC、D、Eを掛け、Kを作るためにBにEを掛ける。
さて、AにAを掛けCを作り、Bを掛けDを作ったから、それゆえにAはBに対し同じようにCはDに対する。propositionⅦ.17
再度、AにBを掛けDを作り、Bにそれを掛けEを作るから、それゆえにBを掛けた数AとBはそれぞれ数DとEを作る。
それゆえにAはBに対し同じようにDはEに対する。しかしAはBに対し同じようにCはDに対し、それゆえにCはDに対し同じようにDはEに対する。propositionⅦ.18
そしてAにCとDを掛けてFとGを作るから、CはDに対し同じようにFはGに対する。propositionⅦ.17
しかしCはDに対し同じようにAはBに対し、それゆえにAはBに対し同じようにFはGに対する。
再度、AにDとEを掛けてGとHを作るから、それゆえにDはEに対し同じようにGはHに対する。しかしDはEに対し同じようにAはBに対する。それゆえにAはBに対し同じようにGはHに対する。 propositionⅦ.17
そしてAとBにEを掛けてHとKを作るから、それゆえにAはBに対し同じようにHはKに対する。しかしAはBに対し同じようにFはGに対し、同じようにGはHに対する。それゆえにFはGに対し同じようにGはHに対し、そして同じようにHはKに対する。propositionⅦ.18
それゆえにC、D、EとF、G、H、KはAがBに対する比で比例している。
次にそれらがそうである最小の数であることをいう。
AとBはそれらと同じ比を持つ最小の数で、同じ比を持つ最小の数は互いに素であるから、それゆえにAとBは互いに素である。proppositionⅦ.22
そして、数AとBにそれぞれそれら自身を掛けて数CとEを作り、それぞれ数CとDを掛けて数FとKを作る。それゆえにC、EとF、Kはそれぞれ互いに素である。propositionⅦ.27
しかし、連続して比例すると同じ数があり、それらの外項が互いに素であるならば、それらはそれらと同じ比を持つ最小の数である。それゆえにC、D、EとF、G、H、KはAとBと同じ比を持つ最小の数である。 propositionⅧ.1
証明終了
系
これから明白である。比例する3つの数がそれらと同じ比を持つ最小の数であるならば、その外項は平方数で、4つの数ならば立方数である。