命題105

「劣線分と通約可能な直線は劣線分である」

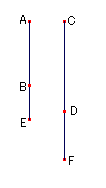
ABを劣線分とし,CDはABと通約可能であるとする。

CDも劣線分であることを示す。

作図は前と同様とする。そのとき，AE,EBは平方において通約可能。よってCFとFDも平方において通約可能である。 �].76 �].13

ここでAEがEBに対するようにCFがFDに対するのでAE上の正方形がEB上の正方形に対するようにCF上の正方形がFD上の正方形に対する。 �X.12 �X.16 �Y.22

よって,合比により,AE上,EB上の正方形の和がEB上の正方形に対するようにCF上,FD上の正方形の和がFD上の正方形に対する。 �X.18

しかしここで，BE上の正方形はDF上の正方形と通約可能。よってAE上,EB上の正方形の和もCF上,FD上の正方形の和と通約可能である。 �X.16 �].11

しかしここで，AE上,EB上の正方形の和は有理,よってCF上,FD上の正方形の和も有理である。 �].76

またAE上の正方形が長方形AE,EBに対するようにCF上の正方形が長方形CF,FDに対する。AE上の正方形はCF上の正方形と通約可能であるので長方形AE,EBも長方形CF,FDと通約可能である。

しかしここで長方形AE,EBは中項,よって長方形CF,FDも中項である。 �].76

よってCF,FDは平方において通約不可能で,それら上の正方形の和は有理でそれらがつくる長方形は有理である。よってCDは劣線分である。 �].75

したがって，劣線分と通約可能な直線は劣線分である。

証明終了

第10巻命題104へ　 第10巻命題106へ　 第10巻目次へ